Gridea

伪随机数的生成在计算机中具有重要的作用，了解一些生成随机数的算法可以帮助我们了解一些计算机底层算法。

特点

伪随机数具有随机性：均匀分布、难以重现

伪随机数生成器

框架

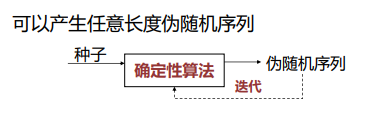
性质

• 伪随机性：与随机数不可区分
• 可重现：相同种子产生相同序列

实例

• srand(s) 设置种子
• rand() 基于种子产生伪随机数

若s一样则会产生相同的伪随机数序列

解决办法：令s = time(NULL)，即让每次调用时种子都不同

time()函数返回unix时间戳

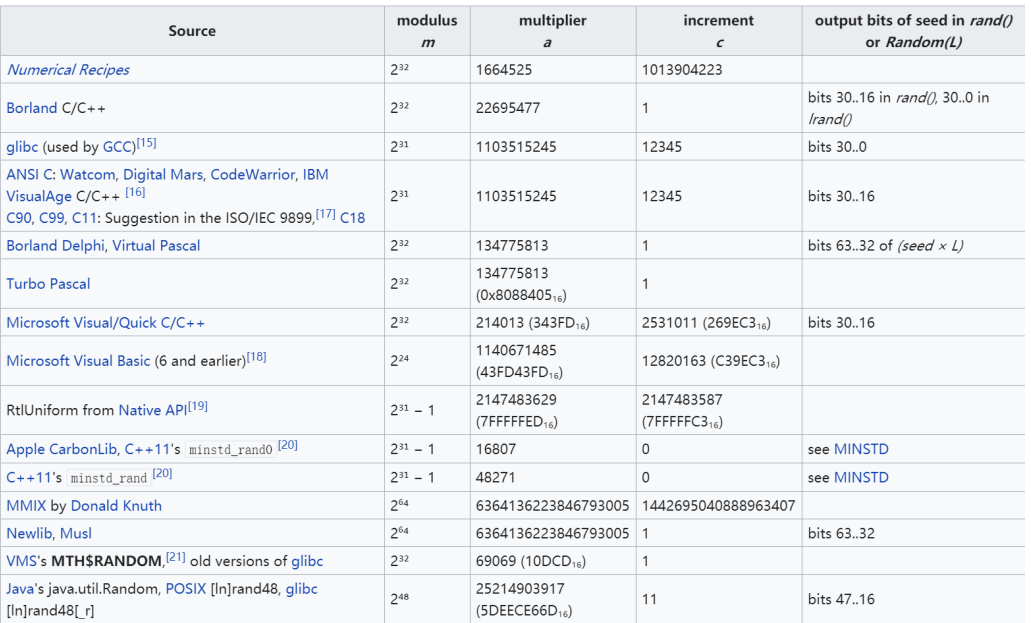
线性同余

早期的rand函数是基于线性同余算法实现的

• 迭代式：Xi+1 = aXi + c mod m
• a(乘数)
• c(增量)
• m(模数)
• X0(种子)

简单实现：

const unsigned int _a = 1103515245;
const unsigned int _c = 12345;
const unsigned int _m = 2147483648; // => 2^31
void lcg_srand(unsigned int seed) {
    // TODO: 设置种子
    _seed = seed;
    // 全局变量默认值：
    //  a = 1103515245
    //  c = 12345
    //  m = 2^31
    //  _seed = 1
}
unsigned int lcg_rand() {
    // TODO：返回一次迭代后的结果，结果值存储在全局变量`_seed`中
    _seed = (_a * _seed + _c) % _m;
    return _seed;
}

安全性

评价标准

• 全周期：{0,1.....,m-1}中任意数都可能被生成i
• 不可预测：无法基于X0，X1，.....，Xi-1推断Xi

显然采用线性同余的方案是没办法满足上述两条标准的

增强方法：使用系统时钟修正增量

BBS-伪随机数生成器

BBS（Blum Blum Shub)

可证明的安全性：可以将区分伪随机数和随机数规约为结束数学难题

线性同余伪随机数生成器不具备可证明的安全性

原理

• 选择素数p和q，满足p mod 4 = q mod 4 = 3
• 模数N = p*q
• 选择种子s，s与N互素

*迭代计算*

示例

• 参数选择p = 11，q = 19，s = 3
• N = 209

迭代计算

X0 = s

X1 = X02 mod N = 9

X2 = X12 mod N = 81

X3 = X22 mod N = 82

......

*选择重要位*

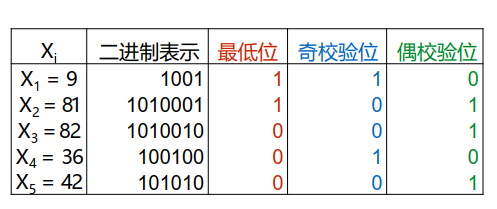
*输出伪随机数*

• 最低位11000 = 24
• 奇校验位10010 = 18
• 偶校验位01101 = 13

简单实现：

unsigned long _bbs_seed = 3;
const unsigned long _p = 11;
const unsigned long _q = 19;
const unsigned long _n = _p * _q;
unsigned int bbs_rand(int flag) {
    // TODO: 返回32轮迭代过后的伪随机数值
    unsigned int ret = 0;
    unsigned int x = _bbs_seed;
    switch (flag)
    {
    case BBS_USE_LAST_BIT:
        for (int i = 0; i < 32; i++)
        {
            ret = ret << 1;
            x = (x * x) % _n;
            if (x & 1 == 1) ret |= 0x00000001;  //若xi最低位为1，则末位补1
        }
        break;
    case BBS_USE_ODD_BIT:
        for (int i = 0; i < 32; i++)
        {
            ret = ret << 1;
            x = (x * x) % _n;
            if (ODD(x)) ret |= 0x00000001;
        }
        break;
    case BBS_USE_EVEN_BIT:
        for (int i = 0; i < 32; i++)
        {
            ret = ret << 1;
            x = (x * x) % _n;
            if (!ODD(x)) ret |= 0x00000001;
        }
        break;
    default:
        break;
    }
    // 全局变量默认值：
    //  p = 11
    //  q = 19
    //  n = p * q
    //  _bbs_seed = 3
    return ret;
}
//奇校验判断
bool ODD(unsigned int x)
{
    int cnt = 0;
    while(x!=0)
    {
        if (x & 1 == 1)  cnt++;
        x = x >> 1;
    }
    //奇数个1返回false
    if (cnt & 1 == 1)   return false;
    return true;
}

小结

BBS的安全性是基于大数难分解困难问题（类似RSA

因此BBS是具有可证明安全性的。